Théorème: (Théorème des valeurs intermédiaires) Soit f: [ a, b] → R une fonction continue sur un segment. Pour tout réel y compris entre f ( a) et f ( b), il existe c ∈ [ a, b] tel que f ( c) = y. Démonstration. Montrons le théorème dans le cas où f ( a) < f ( b). On considère alors un réel y tel que f ( a) ⩽ y ⩽ f ( b) et.. Transcription de la vidéo. bonjour dans cette vidéo ce que je vais faire cet présenter ce qu'on appelle le théorème des valeurs intermédiaires alors au delà de ce nom un petit peu compliqué un petit peu mathématiques tu vas voir qu'en fait c'est un théorème très très intuitif probablement le trm le plus intuitif que tu rencontreras.
![Théorème des Valeurs Intermédiaires TVI Limites et Continuité 2 bac SM [Exercice 6] YouTube](https://i.ytimg.com/vi/uhgdTTuNoSI/maxresdefault.jpg "Théorème des Valeurs Intermédiaires TVI Limites et Continuité 2 bac SM [Exercice 6] YouTube")
Théorème des Valeurs Intermédiaires TVI Limites et Continuité 2 bac SM [Exercice 6] YouTube
![Limites et Continuité Théorème des Valeurs Intermédiaires 2 Bac S.ex [Exercice 41] YouTube](https://i.ytimg.com/vi/ptzY8_azJc0/maxresdefault.jpg "Limites et Continuité Théorème des Valeurs Intermédiaires 2 Bac S.ex [Exercice 41] YouTube")
Limites et Continuité Théorème des Valeurs Intermédiaires 2 Bac S.ex [Exercice 41] YouTube
Démonstration du théorème des valeurs intermédiaires AlloSchool
![Théorème des Valeurs Intermédiaires TVI 2 Bac SM [Exercice 18] YouTube](https://i.ytimg.com/vi/m_6dcRWeooc/maxresdefault.jpg "Théorème des Valeurs Intermédiaires TVI 2 Bac SM [Exercice 18] YouTube")
Théorème des Valeurs Intermédiaires TVI 2 Bac SM [Exercice 18] YouTube
Théorème des Valeurs Intermédiaires Exercice 2 YouTube
Le théorème des valeurs intermédiaires exercices corrigés Partie 2 YouTube
théorème des valeurs intermédiaire YouTube
Théorème des Valeurs Intermédiaires TVI Continuité d'une Fonction 2 Bac S.ex [Exercice 27
Théorème des valeurs intermédiaires. T.V.I. Logamaths.fr
Exercice sur les fonctions (TES) Théorème des valeurs intermédiaires YouTube
Continuité Théorème des valeurs intermédiaires (TVI) YouTube
Fiche BAC S 03 Term S Théorème des valeurs Intermédiaires (thvi)
theoreme des valeurs intermediaires YouTube
Théorème des valeurs intermédiaires YouTube
Exercices Le théorème des valeurs intermédiaires YouTube
Comment appliquer le théorème des valeurs intermédiaires et son corollaire ? YouTube
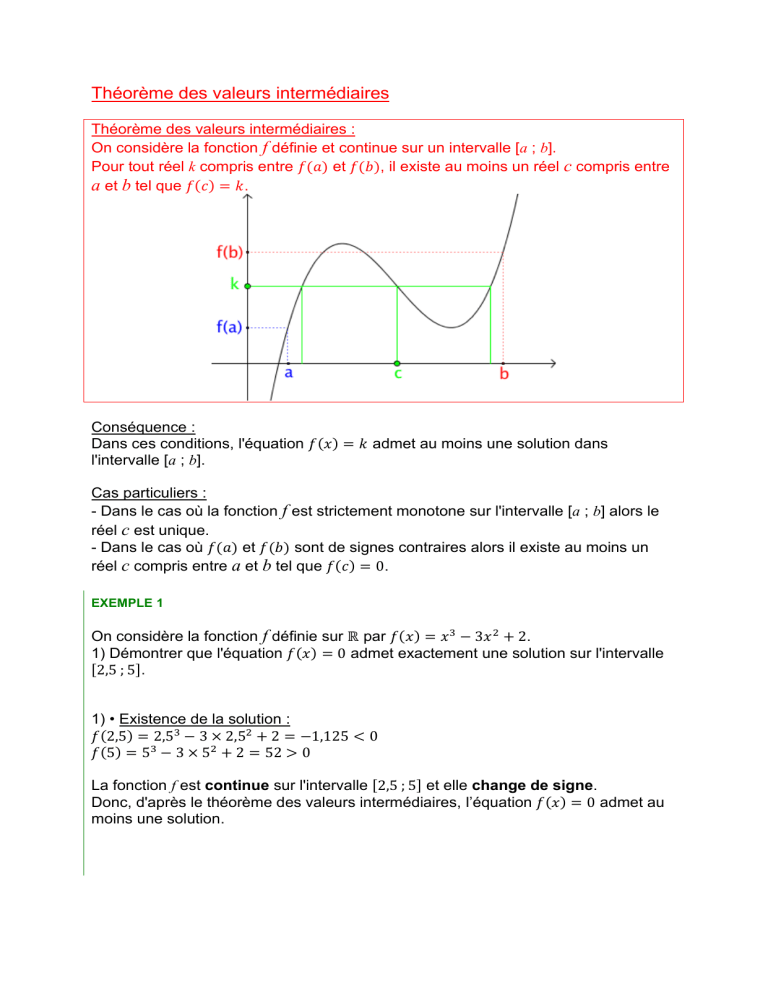
Théorème des valeurs intermédiaires
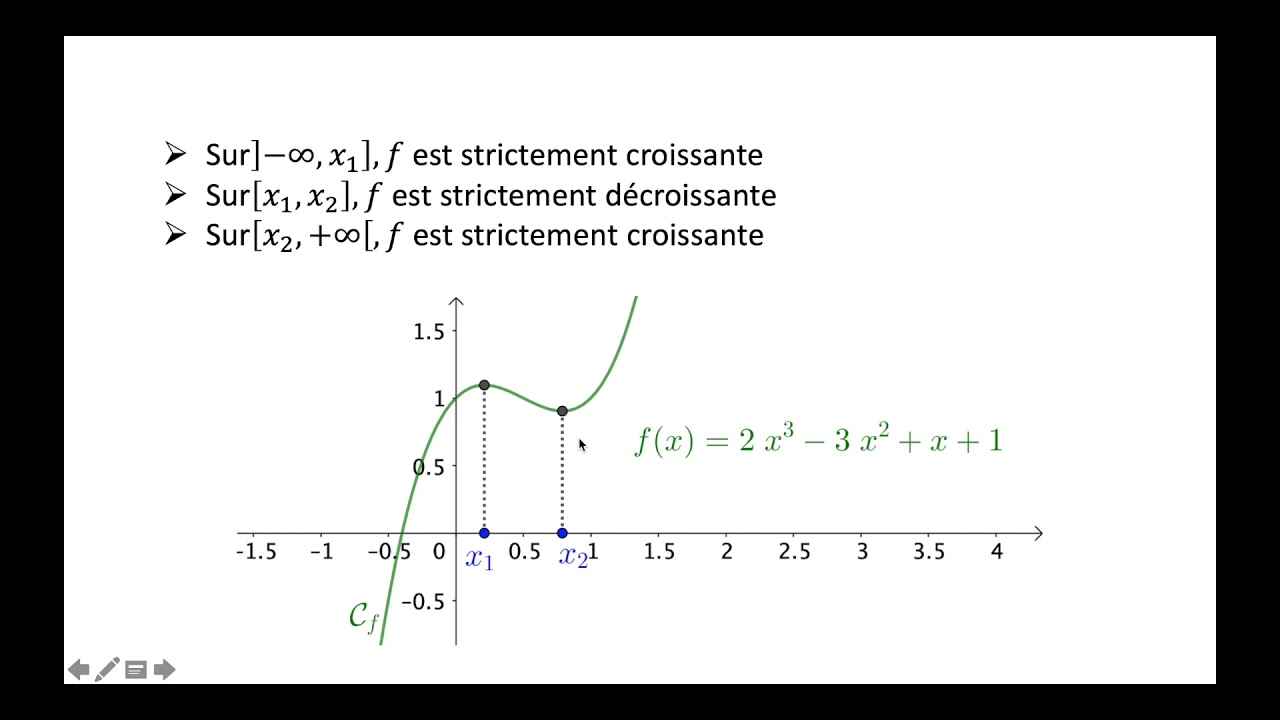
Utilisation du théorème des valeurs intermédiaires (TVI) et solutions approchées d'équations
Comment utiliser le théorème des valeurs intermédiaires ? Terminale S Exercice corrigé
théorème des valeurs intermédiaires lien avec les équations exercice type Bac YouTube
Théorème - Résolution graphique et encadrement de xB. 1. Théorème des valeurs intermédiaires appliqué aux fonctions strictement monotones. Si la fonction f est continue et strictement monotone (croissante ou bien décroissante) sur [ a ; b] et si le réel m est compris entre f (a) et f (b), alors l'équation f ( x) = m a une seule.. Les Exercices corrigés de la théorème des valeurs intermédiaires. Exercice 1. Soit la fonction définie sur par x3-x²-x+1. 1) Montrer que la fonction f est continue sur [-1 ;2]. 2) Calculer f (-1) et f (2) 3) En déduire que l'équation f (x) = 5 admet au moins une solution dans [-1 ; 2]. Voir aussi: La Fonction Logarithme Népérien.
